Visualizza articoli per tag: matematica
4 aprile 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole
Durata: 120 minuti
20 marzo 2024
Verifica di matematica, classe seconda liceo scientifico
Argomento: equazioni di secondo grado
Durata: 60 minuti
21 marzo 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole
Durata: 120 minuti
20 febbraio 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: circonferenza
Durata: 120 minuti
17 febbraio 2024
Verifica di matematica, classe seconda liceo scientifico, recupero per assenti
Argomento: calcolo delle probabilità
Durata: 60 minuti
Probabilità ed educazione civica
Il calcolo delle probabilità è parte integrante del programma di matematica del liceo scientifico: dopo un primo approccio in seconda, con un cenno al Teorema di Bayes, si procede, in quarta, con un approfondimento, grazie ai nuovi strumenti offerti dal calcolo combinatorio e ad una maggiore capacità di astrazione.
Il calcolo delle probabilità è anche estremamente utile per affrontare un percorso di educazione civica e il collegamento più immediato ha a che fare con l’azzardopatia, anche se, in generale, la probabilità ci offre un modo di interpretare la realtà, entrando nelle aule di tribunale, negli ospedali e nelle decisioni che prendiamo ogni giorno.
Ho cominciato il percorso con i miei alunni di seconda sfruttando il lavoro di Taxi1729, una società di consulenza, formazione e comunicazione scientifica, il cui lavoro, come recita l’homepage, ha «un unico filo conduttore: la decisione umana». Il primo video, Gratta e vinci: compulsivi per legge, mostra fin da subito che ci sono studio e pianificazione dietro la forza del gioco d’azzardo.

«Nel 1997, in una relazione alla Camera dei deputati sull’andamento dei Gratta e Vinci, il Ministro delle Finanze Visco si dichiara soddisfatto degli ultimi incassi ottenuti per lo Stato e fa una lista dei punti di forza di questo gioco, su cui investire negli anni successivi». I punti di forza sono l’intimità, data dal sentirsi protagonista del gioco, l’illusione della vincita, perché come lascia capire la pubblicità è facile vincere, le piccole vincite, visto che un biglietto su quattro è vincente, e le quasi vincite, che generano frustrazione, ma fanno anche venir voglia di riprovarci subito. Anche i mass media sono complici di questi incassi dello Stato, perché ogni volta che c’è una grande vincita, questa viene enfatizzata, invogliando gli spettatori a diventare giocatori, a tentare la fortuna. Anche se siamo consapevoli che le probabilità di vincita sono molto basse, il fatto che qualcuno vinca ogni tanto ci porta a illuderci di poter essere, un giorno, uno dei fortunati vincitori.

Insegno a Lovere, sul Lago d’Iseo, e sono a pochi minuti di auto da Rovetta (in provincia di Bergamo) dove «è stato centrato il 6 dei record al SuperEnalotto!» il 16 febbraio del 2023. Il giorno dopo, Paolo Canova e Diego Rizzuto di Taxi1729 hanno pubblicato il video Qui vinti 371 milioni di euro! proprio per parlare della vincita. Quando ho fatto il percorso con la seconda dell’anno scorso, la vincita è stata realizzata proprio il giorno che i miei alunni affrontavano la verifica scritta sull’argomento e il giorno della consegna ho mostrato il video. Come ricorda Diego verso la fine, quel 16 febbraio ha coinciso con «il 21° Bradbury day, ovvero il ventunesimo anniversario (a proposito di improbabilità) della improbabilissima vittoria olimpica del pattinatore australiano Steven Bradbury», vincitore della prima medaglia d’oro australiana alle Olimpiadi invernali.

La vittoria è stata così inaspettata per tutti che “doing a Bradbury” in Australia è diventato un modo di dire che indica «un successo clamoroso e altamente insperato». Allo stesso livello si pone quanto successo a Randy Johnson, che ha colpito un colombo lanciando una palla durante una partita di baseball, il 24 marzo 2001. Anche questo evento è altamente improbabile, e consapevolmente Randy ha usato l’unicità di quanto successo per farne il suo logo, ora che esercita la professione di fotografo.
Nel percorso sulla probabilità è per me estremamente importante sottolineare come il nostro intuito non sempre ci aiuti ad affrontare le situazioni: spesso ci porta fuori strada, spingendoci a valutare erroneamente la probabilità di un evento. Ho continuato il percorso, quindi, parlando del paradosso di Monty Hall, che poi non è altro che un’applicazione del teorema di Bayes. Ho cominciato con un piccolo estratto del film 21, nel momento in cui il professore Mickey Rosa capisce che l’allievo del MIT Ben Campbell potrebbe essere un ottimo acquisto per la squadra che sta addestrando a vincere ai tavoli del Blackjack. Il professore offre a Ben «l’occasione di beccarsi un credito extra», parlando di quello che lui chiama «il problema del conduttore di quiz televisivo»: «Ben, diciamo che stai giocando in televisione e hai la possibilità di scegliere fra tre porte diverse, intesi? Dunque: dietro una delle porte c’è un’auto nuova, dietro le altre due: capre!» Sul sito Mathigon si può procedere con una simulazione del gioco e io lo faccio in classe, offrendo alla classe anche l’occasione di ripassare un po’ l’inglese. Una volta che è stata effettuata la scelta, il presentatore apre una delle porte non scelte e dietro la quale c’è, ovviamente, una capra. A questo punto del gioco, è più conveniente tenere la prima scelta o cambiare porta? Ben non ha dubbi e dà la risposta giusta, ma a me piace procedere leggendo la descrizione che ne fa Christopher, il protagonista del libro di Mark Haddon Lo strano caso del cane ucciso a mezzanotte, perché offre anche l’occasione di riflettere su come funzioni la matematica: «Il signor Jeavons disse che mi piaceva la matematica perché mi faceva sentire al sicuro. Disse che mi piaceva perché la matematica serve a risolvere i problemi, poi aggiunse che questi problemi erano difficili e interessanti, ma che alla fine c’era sempre una risposta chiara e diretta per tutto. Ciò che intendeva era che la matematica non è come la vita perché nella vita non esistono risposte chiare e dirette. So che era questo che voleva dire perché è quello che ha detto. Perché il signor Jeavons non capisce i numeri». Per questo motivo, il capitolo 101 del libro (ovvero il 26°) è dedicato al paradosso di Monty Hall, che viene esplorato nel dettaglio, insieme alla vicenda di Marilyn vos Savant, che aveva spiegato il problema dalle pagine della rivista americana «Parade». La sua risposta giusta le è costata un forte attacco, visto che molti scrissero alla rivista contestando la sua risposta: «Il 92% delle lettere sostenevano che si era sbagliata, e molte provenivano da matematici e scienziati». Roberto Natalini, dalle pagine del libro Teorema di Bayes, ci ricorda che «persino il famoso matematico Paul Erdős pensava inizialmente che la soluzione proposta da Selvin e vos Savant fosse sbagliata» (Steve Selvin è lo statistico che risolse il problema per la prima volta nel 1975, e il fatto che lui non sia stato attaccato pesantemente come la vos Savant mi spinge a pensare che parte dell’attacco sia imputabile a una questione di genere).

Per continuare a lavorare sui bias cognitivi legati alla probabilità, chiedo ai miei alunni di mettersi in gioco con il test proposto da Paolo Canova e Diego Rizzuto nel libro Fate il nostro gioco: ci sono 10 eventi diversi e gli alunni devono metterli in ordine, dal più probabile al meno probabile. Non è certo facile procedere senza calcoli e senza ricerche in rete, usando solo l’intuito: «Nei numerosi incontri che abbiamo fatto in giro per l’Italia, nessuno ha mai indovinato l’ordine giusto. Un po’ perché di alcune di queste cose sappiamo poco o niente, dunque facciamo fatica a stabilirne la probabilità, un po’ perché è molto difficile sottrarsi all’influenza delle speranze, delle paure, delle esperienze passate, dell’amplificazione mediatica o al nostro naturale istinto di accordarci alle opinioni altrui», dichiarano i due autori.
Parlando di nuovo del SuperEnalotto, non posso non dare ascolto ad un’altra voce autorevole nel campo dell’azzardopatia, Federico Benuzzi, docente, giocoliere, attore, autore del libro La legge del perdente e autore e protagonista dello spettacolo teatrale L’azzardo del giocoliere, di cui il video A cosa serve la matematica? Il SuperEnalotto non è che un estratto.

In modo molto coinvolgente, Federico Benuzzi descrive la vittoria al SuperEnalotto come la scelta di una carta, precedentemente firmata, in un mazzo con 600 milioni abbondanti di carte. Immaginando di mettere in fila tutte le carte, in un serpentone di 311 km, che si snoda da Bologna al casinò di Locarno, «camminate accanto al mazzo e quando finalmente siete paghi, vi fermate, vi chinate, ne pescate una e se è quella che avete scelto avete vinto 130 milioni di euro». Nonostante l’improbabilità che questo avvenga, «il fatturato del gioco d’azzardo, in Italia, è circa 90 miliardi l’anno! Quasi l’8% del PIL! […] Si stima che gli italiani spendano, in gioco d’azzardo, il 10% di quello che spendono come privati!»
In questa passeggiata tra le probabilità, mi piace fare riferimento a storie che in qualche modo possano restare impresse e che aiutino, quindi, a collocare meglio quanto dico dal punto di vista matematico. Per questo motivo, non può mancare Roy Sullivan, del quale ho sentito parlare per la prima volta quando ho visto online la conferenza di Paolo Canova e Diego Rizzuto al Salone del libro nel 2013. L’ho ritrovato, ovviamente, anche tra le pagine del loro libro, nel capitolo dedicato agli eventi improbabili, come «manifestazione empirica che l’improbabilità esiste e vive insieme a noi».

Roy Sullivan è un guardiaparco, che, nell’arco della sua vita, è stato colpito sette volte da un fulmine, a dimostrazione del fatto che anche ciò che indichiamo come «praticamente impossibile» potrebbe verificarsi. Nel corso della conferenza, la vicenda di Roy Sullivan è presentata per rispondere all’obiezione di chi potrebbe riconoscere che per quanto la vittoria al SuperEnalotto sia «praticamente impossibile», è fuor di dubbio che qualcuno, ogni tanto, vince! Diego e Paolo citano la legge dei numeri grandi, per sottolineare che anche se la probabilità di vincere, per il singolo, è molto bassa, quando ci sono molte persone che giocano, la probabilità che, all’interno della popolazione, qualcuno vinca potrebbe essere anche molto alta. In altre parole, se in un gruppo di cinque persone lanciamo un dado a sei facce e ognuno di noi scommette su una faccia diversa, la probabilità che qualcuno di noi riesca a vincere è molto alta (5/6), mentre la probabilità del singolo non è cambiata (1/6).
Torno poi alle fasi iniziali della conferenza e lascio che Diego e Paolo raccontino l’incredibile vicenda del processo di O.J. Simpson, ripresa anche da Paolo Caressa in un articolo pubblicato su Prisma, La probabilità condizionata del Reverendo. La vicenda è quella del processo che ha fermato gli USA quando, il 3 ottobre 1995, stava per essere emanato il verdetto: O.J. Simpson era accusato di aver ucciso la ex moglie, Nicole Brown Simpson, ma alla fine del processo verrà giudicato “Not guilty!”, non colpevole. L’accusa aveva dimostrato la presenza di violenze domestiche durante il loro matrimonio, sposando la tesi secondo la quale, essendo un uomo violento, era molto probabile che fosse lui il responsabile della morte della ex moglie. La difesa, gestita dal cosiddetto Dream Team, ovvero il gruppo di avvocati migliore sulla piazza, aveva quindi proceduto con il calcolo delle probabilità, studiando le cifre dell’anno precedente: su 4 milioni di donne picchiate dal partner, “solo” 1600 erano state uccise, ovvero lo 0,04%, quindi era estremamente improbabile che O.J. Simpson fosse il responsabile della morte della ex moglie. Un dream team per l’accusa, con almeno un matematico, avrebbe forse potuto ribaltare il verdetto: c’è un errore macroscopico alla base del ragionamento, perché l’insieme di riferimento, ovvero l’insieme dei casi possibili, non può essere quello delle donne picchiate dal partner. Alla luce di quanto successo, l’insieme di riferimento deve essere quello delle donne che hanno subito violenza domestica E che sono state uccise. A questo punto, con questo nuovo insieme al denominatore costituito da 1800 donne, la probabilità diventa 1600/1800, ovvero dell’89%. Il Reverendo Bayes avrebbe potuto aiutare gli avvocati a fare realmente giustizia.

In classe, è stato necessario anche dedicare un po’ di tempo al calcolo, esplorando la teoria della probabilità attraverso alcuni esercizi, per capire ancora meglio i problemi che ci eravamo posti. Ho usato il libro del prof. Daddi Calcolo delle probabilità come supporto, ma ho avuto modo di utilizzare anche gli esempi proposti da Roberto Natalini nel suo libro Teorema di Bayes, pubblicato nella Collana di Le Scienze. Ci siamo divertiti con Il problema dei gattini, dove «una gatta ha partorito due gattini di cui almeno uno è maschio. Qual è la probabilità che anche l’altro sia maschio»?, che è indicato come un paradosso. Poi non ho potuto non parlare del problema dei test diagnostici e, seguendo le orme di Roberto Natalini, ne ho presentata una soluzione elementare, sottolineando come «la probabilità per una persona malata di essere positiva è diversa dalla probabilità per una persona positiva di essere malata».
In conclusione, sono tornata sul gioco d’azzardo con il video di Taxi1729 Il caso si fa bello.

Questa volta in scena ci sono Diego Rizzuto e Olmo Morandi: tutto comincia al casinò di Montecarlo, il 18 agosto del 1913, quando le persone che si trovarono davanti al tavolo della roulette videro uscire 19 neri consecutivi. Su cosa avreste puntato per il ventesimo lancio? Avreste fatto come i presenti e vi sareste giocati anche le scarpe? «La forza di un’anomalia come questa è capace di indurre in tentazione chiunque, persino i più scettici», dichiarano Paolo e Diego nel libro, e nel video sentiamo una fastidiosa vocina che continua a ripetere «Il rosso è più probabile!» Ma il rosso si negò ancora e i neri consecutivi arrivarono a 26. Il motivo per cui avremmo puntato sul rosso è legato all’idea errata di caso che abbiamo in testa: secondo gli psicologi Daniel Kahneman e Amos Tversky «tutti noi abbiamo in testa delle regole estetiche che il caso deve rispettare per potersi dire tale!». L’equità, l’alternanza e il disordine appartengono a quei bias cognitivi di cui siamo tutti vittime, in qualche modo, come dimostrato da Steve Jobs, che, con l’opzione shuffle dell’iPod «decise di correre ai ripari e di creare una riproduzione casuale non “veramente casuale”, ma che apparisse tale ai clienti».
Queste regole estetiche sono così radicate che trovano terreno fertile anche nel gioco del Lotto, con i numeri ritardatari, che sono riportati anche nel sito ufficiale del gioco del Lotto (quelli seguenti sono comparsi il 16 febbraio 2024):
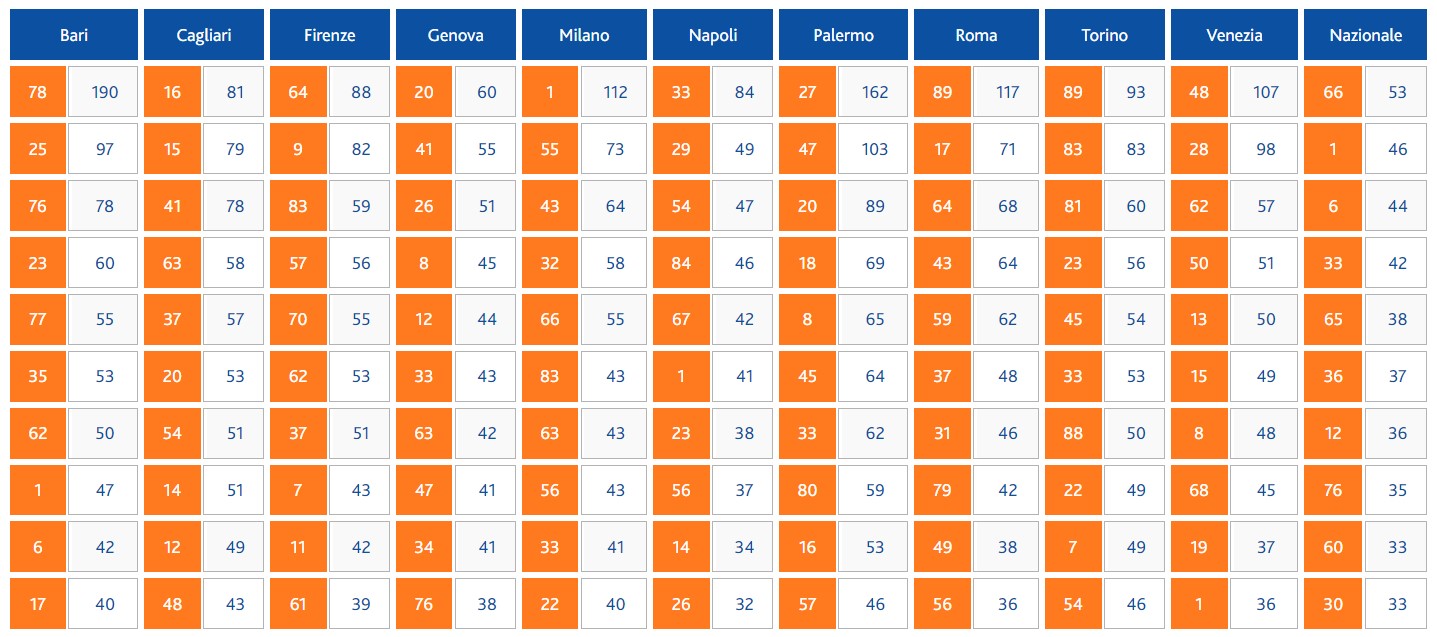
Tendiamo a vedere una dipendenza tra i singoli eventi, ma non tutti gli eventi sono collegati tra loro, e sicuramente non sono collegate tra loro le estrazioni del Lotto. Il Lotto non ha memoria, come la moneta, come i dadi, come la roulette!
Dopo aver cercato di scardinare i bias cognitivi legati alla probabilità a suon di matematica, ho concluso il percorso riprendendo in mano l’articolo (già citato) di Paolo Caressa per parlare di un’altra vicenda giudiziaria complicata dal calcolo (errato) della probabilità, quella «dell’inglese Sally Clark, condannata nel 1999 per aver soffocato entrambi i figli: il giudice aveva stimato troppo improbabile che tutti e due fossero morti in culla, dato che la probabilità che un bimbo muoia di questa orribile sindrome era stimata 1 su 8543». Se noi consideriamo indipendenti tra loro le due morti, come ha fatto il pediatra interpellato, la probabilità, già bassa, di un singolo evento, diventa ancora più bassa quando si considerano i due eventi insieme, «poco più di un milionesimo per cento!» Bisogna aspettare il 2001 per avere l’intervento della Royal Statistical Society, che screditò l’ipotesi del pediatra: «la probabilità della morte in culla di un bambino è ben più alta se un suo fratello ha pure subito questa terribile sorte». Sally Clark venne scagionata nel 2003, ma la sua vita era ormai stata rovinata. Non ha avuto la fortuna di avere dalla sua parte il Dream Team di O.J. Simpson…
Fatto in questo modo, il percorso ha permesso di guardare in faccia i nostri bias cognitivi, dare alla teoria delle probabilità una parvenza umana attraverso il racconto di numerosi aneddoti, impedire che venisse percepito come mero calcolo, mostrare, ancora una volta, che la matematica è ovunque e che per l’educazione civica è una vera fonte di ispirazione!
Verso il futuro
Durante tutto il processo di analisi dei dati, ci siamo resi conto di ciò che avremmo dovuto cambiare, in parte per semplificare il nostro lavoro e in parte per rendere ancora più attendibile la nostra indagine statistica, evitando ambiguità:
- prima di diffondere il sondaggio, potrebbe essere utile farlo compilare ad alcune persone, per valutare la chiarezza delle domande e poter, quindi, procedere con eventuali correzioni;
- formulare delle domande chiuse, semplici, chiare e senza una dubbia interpretazione per evitare errori da parte di chi deve compilare il sondaggio; ridurre il più possibile le risposte aperte per rendere più facile l’analisi dei dati;
- nel caso dell’impiego, inserire delle opzioni di risposta che consentano di ricondurre facilmente la professione alle categorie indicate dall’ISTAT;
- una domanda che abbia per risposta “spesso” o “qualche volta” risulta poco oggettiva: dovremmo precisare quanto è “spesso” dal nostro punto di vista (tutti i giorni? Più volte al giorno?).
Queste riflessioni si riveleranno particolarmente utili nel momento in cui procederemo alla stesura di un nuovo questionario, avente per oggetto la matematica nella quotidianità.
IL NUOVO QUESTIONARIO
Nell’ottica di mettere a frutto quanto imparato con questa indagine e con l’obiettivo di realizzare un nuovo questionario (che però verrà somministrato e analizzato da un’altra classe), ci siamo concentrati sulla presenza della matematica nella nostra vita quotidiana. Nel proporre il questionario non abbiamo potuto non tenere conto di alcuni aspetti legati anche all’ambito lavorativo, perché riteniamo che in qualche modo questo possa influenzare l’uso che se ne fa nel resto della giornata. È più probabile che ricorra alla matematica per la soluzione di problemi quotidiani un docente di matematica, ad esempio, rispetto a qualcuno il cui lavoro non ne prevede una grande applicazione. Per la formulazione delle domande, e soprattutto delle scelte multiple, abbiamo riflettuto sulle varie azioni e sui singoli momenti della giornata, per poter capire quanto la matematica sia parte della nostra vita. Abbiamo analizzato anche le diverse branche della matematica per capire quali potessero essere le loro applicazioni, chiedendo aiuto ad altre persone per arricchire la casistica, in modo anche da avere un’idea di quanto la gente possa essere consapevole delle applicazioni quotidiane.
Per le prime domande, ci siamo volute soffermare su due informazioni personali che abbiamo ritenuto importanti, ovvero il grado di istruzione e la fascia d’età, per poter valutare l’impiego della matematica in funzione del proprio titolo di studio. Per i quesiti successivi, ci siamo concentrate su richieste generali che ci aiuteranno a comprendere quanto la matematica sia riconosciuta dalle persone. La prima domanda è una versione quotidiana di quella proposta alla fine del precedente questionario: al posto di «Pensa che potrebbe lavorare senza matematica?», abbiamo proposto «Pensa che la sua vita sarebbe uguale se non ci fosse la matematica?», mentre la domanda successiva chiede di quantificare l’utilizzo della matematica nella quotidianità.
«Che cosa applica della matematica nel suo lavoro?» è diventata: «In quali attività utilizza di più la matematica?» e abbiamo proposto alcune risposte, collegando l’argomento matematico a un esempio tratto dalla quotidianità. Per trovare le possibili risposte a questa domanda e chiarire i dubbi che ci erano sorti, abbiamo chiesto ai nostri genitori e a conoscenti in quali attività ritenevano che questa disciplina fosse fondamentale: valutare le offerte al supermercato, gestire le finanze personali, modificare una ricetta per adeguarla al numero di persone usando le proporzioni… Tra le alternative possibili abbiamo messo anche i viaggi e lo sport, pensando ai fusi orari, al cambio monetario e alle combinazioni delle squadre durante i tornei.
Abbiamo ritenuto fosse il caso di chiedere con quale frequenza venga usata la calcolatrice per risolvere semplici problemi aritmetici, pensando alle ricette o alla suddivisione del conto in pizzeria, per riuscire a cogliere quanta dimestichezza abbiano le persone con la matematica.
Quella più bella, a nostro modo di vedere, è quella riguardante le differenti competenze matematiche a seconda del luogo in cui si vive: siamo consapevoli che esista una matematica diversa a seconda del contesto in cui si vive, basta confrontare tra loro una tribù indigena e un tipico abitante di New York e ci piacerebbe vedere quale potrebbe essere la risposta a questa domanda.
Ci sono anche tante altre domande, ma non è il caso di rovinarvi la sorpresa…
Conoscenze adeguate?
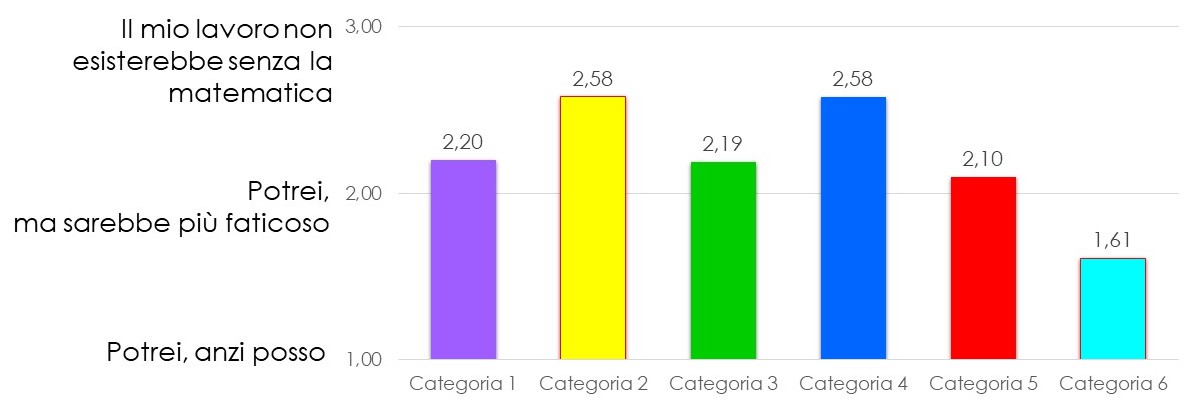
La domanda numero 6 del questionario ha a che fare con il bagaglio di conoscenze fornito dalla scuola: «La scuola che ha frequentato le ha fornito un bagaglio di conoscenze matematiche adeguato rispetto a quello che deve fare?». Le risposte a disposizione erano cinque:
- Non uso la matematica nel mio lavoro
- Per la matematica che uso, bastavano le elementari!
- Le conoscenze che ho NON sono adeguate: avrei dovuto fare un'altra scuola
- Le conoscenze che ho NON sono adeguate: avrei dovuto studiare di più
- Le conoscenze che ho sono adeguate
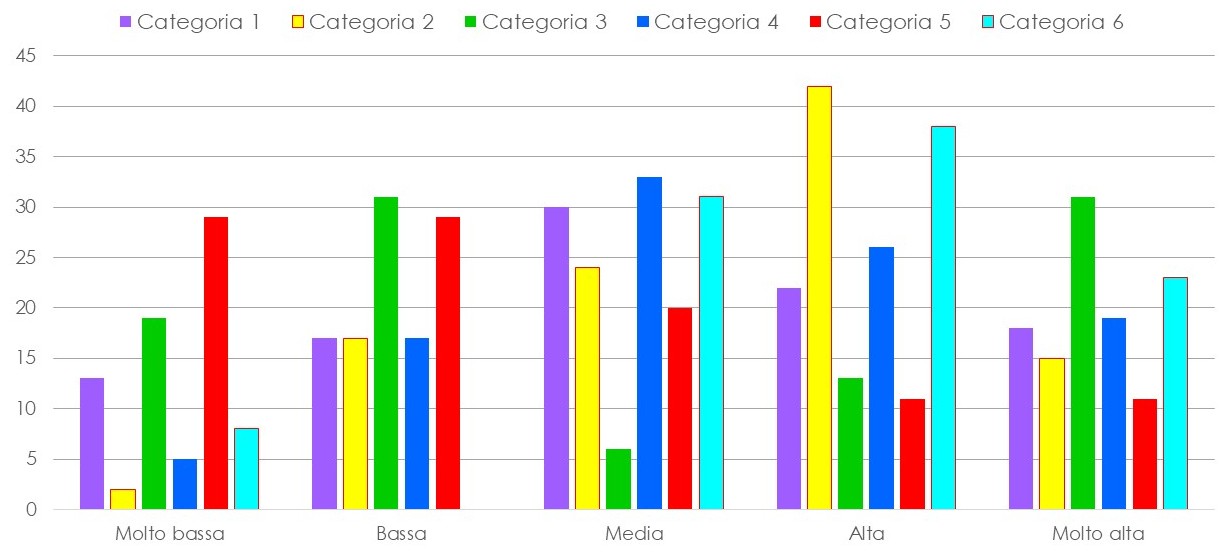
A queste 5 risposte è stato assegnato un punteggio da 1 a 5 a partire dalla prima, e poi è stata fatta la media per ricavare il grafico seguente.
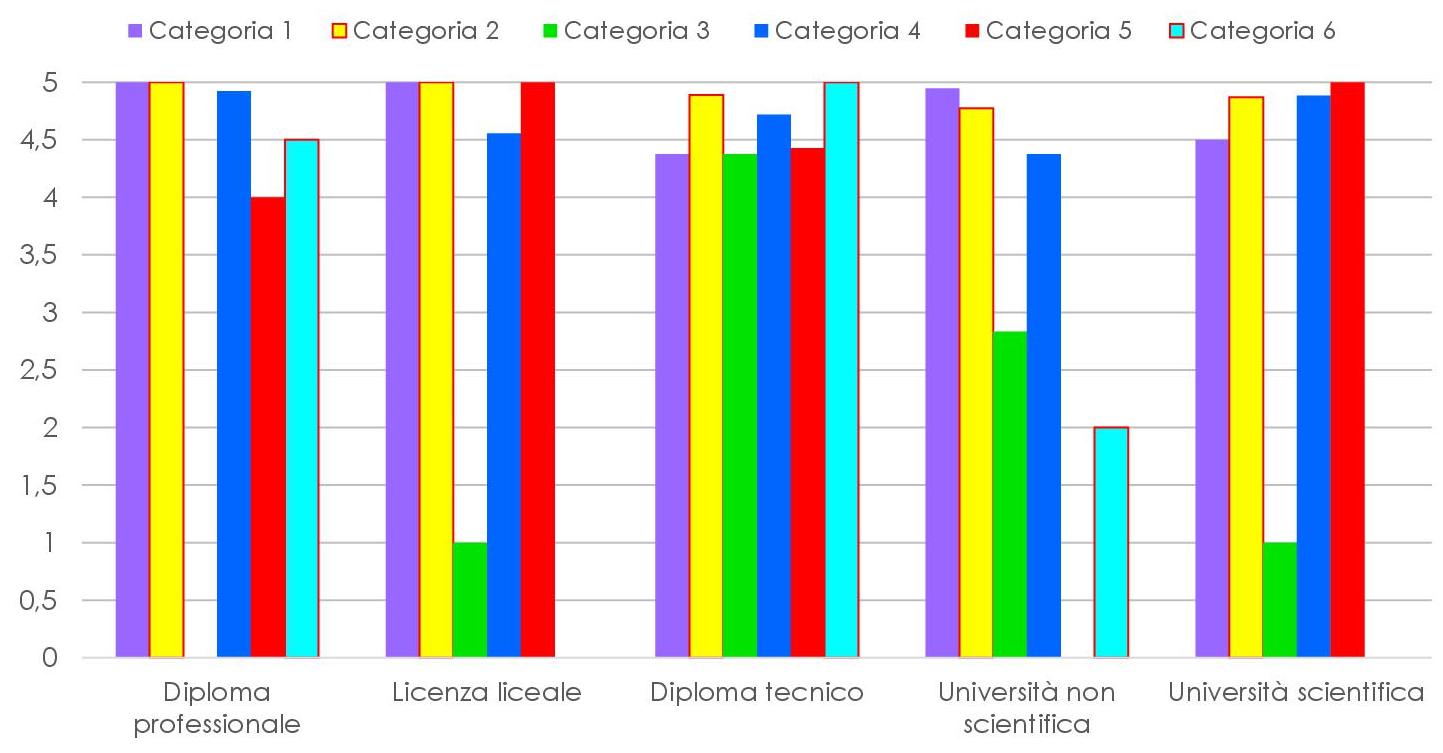
Cerchiamo di interpretarlo dando rilevanza al titolo di studio, riportato in ascissa, mentre i colori riportano l’attenzione sulle categorie. Prima di addentrarci nella descrizione, facciamo alcune precisazioni:
- il commento che segue non vuole essere un giudizio sulla scuola
- come evidenziato nel primo paragrafo, alcune professioni hanno visto un cambio di titolo di studio
- il livello di adeguatezza è percepito, non giudicato obiettivamente
- il percorso professionale scelto, come evidenziato nel paragrafo precedente, è stato fortemente influenzato dal proprio rapporto con la matematica
Analizziamo i risultati, usando due diversi raggruppamenti: prima consideriamo il livello scolastico e poi la categoria.
- Diploma professionale: coloro che hanno risposto al questionario si riconoscono una preparazione matematica adeguata al percorso scelto. Questo potrebbe rispecchiare la realtà delle scuole professionali, dove si addestrano gli studenti a svolgere lavori più che altro pratici, che non richiedono grandi competenze matematiche.
- Licenza liceale: spicca la colonna della terza categoria: si tratta di un’unica risposta, data da un’educatrice, che dichiara di non usare la matematica nel proprio lavoro. Al netto di questa risposta, possiamo dire che la licenza liceale dà competenze matematiche adeguate.
- Diploma tecnico: gli istituti tecnici forniscono conoscenze matematiche adeguate al lavoro per la maggior parte dei propri studenti. Questo potrebbe restituirci il quadro di una scuola che istruisce i propri studenti con competenze matematiche specifiche per il lavoro che dovranno affrontare.
- Università non scientifiche: sembra che le categorie 3 e 6 siano quelle più problematiche: per la categoria 3, le lauree non scientifiche corrispondono a sei educatrici, che hanno risposto come segue: due hanno dichiarato di avere conoscenze matematiche adeguate, una ha risposto di non usare la matematica nella sua professione e tre hanno dichiarato di usare la matematica elementare. Per la categoria 6, si tratta di un’operaia agricola, che dichiara sufficiente la matematica elementare per il suo lavoro.
Se consideriamo il risultato nel suo complesso, possiamo notare che la maggior parte dei laureati sostiene di possedere conoscenze matematiche adeguate al mondo del lavoro, mentre per gli altri, vale il fatto che il percorso scolastico non dà rilevanza alla matematica, che effettivamente non sempre viene usata sul fronte professionale. - Università scientifica: sembra che le conoscenze siano adeguate, tranne che per la categoria 3: si tratta di un’educatrice che ha dichiarato di non usare la matematica nel suo lavoro. Per il resto non ci sono grandi sorprese: è forse scontato ritenere che le facoltà scientifiche preparino gli studenti in maniera adeguata dal punto di vista matematico, ma è bello vederlo confermato dal nostro campione.
Concentrandoci sui colori, ovvero sulle singole categorie, possiamo avere un diverso punto di vista:
- Categoria 1: il primo gruppo comprende avvocati, dirigenti e imprenditori. I ruoli dirigenziali richiedono competenze matematiche, che coinvolgono il processo decisionale, l’analisi dei dati e la lettura dei grafici, mentre per quanto riguarda gli avvocati, è altro ad avere più peso. Il grafico ci dice che chi appartiene a questa categoria ritiene di avere competenze matematiche adeguate.
- Categoria 2: si tratta di consulenti, ingegneri, medici e commercialisti e il grafico evidenzia che tutti coloro che hanno risposto al questionario ritengono di avere competenze matematiche adeguate.
- Categoria 3: al nostro questionario hanno risposto principalmente educatrici e agenti di commercio. In entrambi i casi, si tratta di professioni basate più che altro su competenze relazionali, perciò le competenze matematiche non sono molto richieste o basta la matematica elementare.
- Categoria 4: gli impiegati che hanno risposto al nostro questionario si riconoscono competenze matematiche adeguate.
- Categoria 5: a parte il caso dell’operaia agricola richiamata sopra, a questa categoria appartengono diplomati che per la maggior parte dichiarano di avere competenze matematiche adeguate.
- Categoria 6: si parla di artigiani e operai specializzati, che dichiarano di avere competenze matematiche adeguate.
Concludi con le Prospettive future
Il rapporto con la matematica
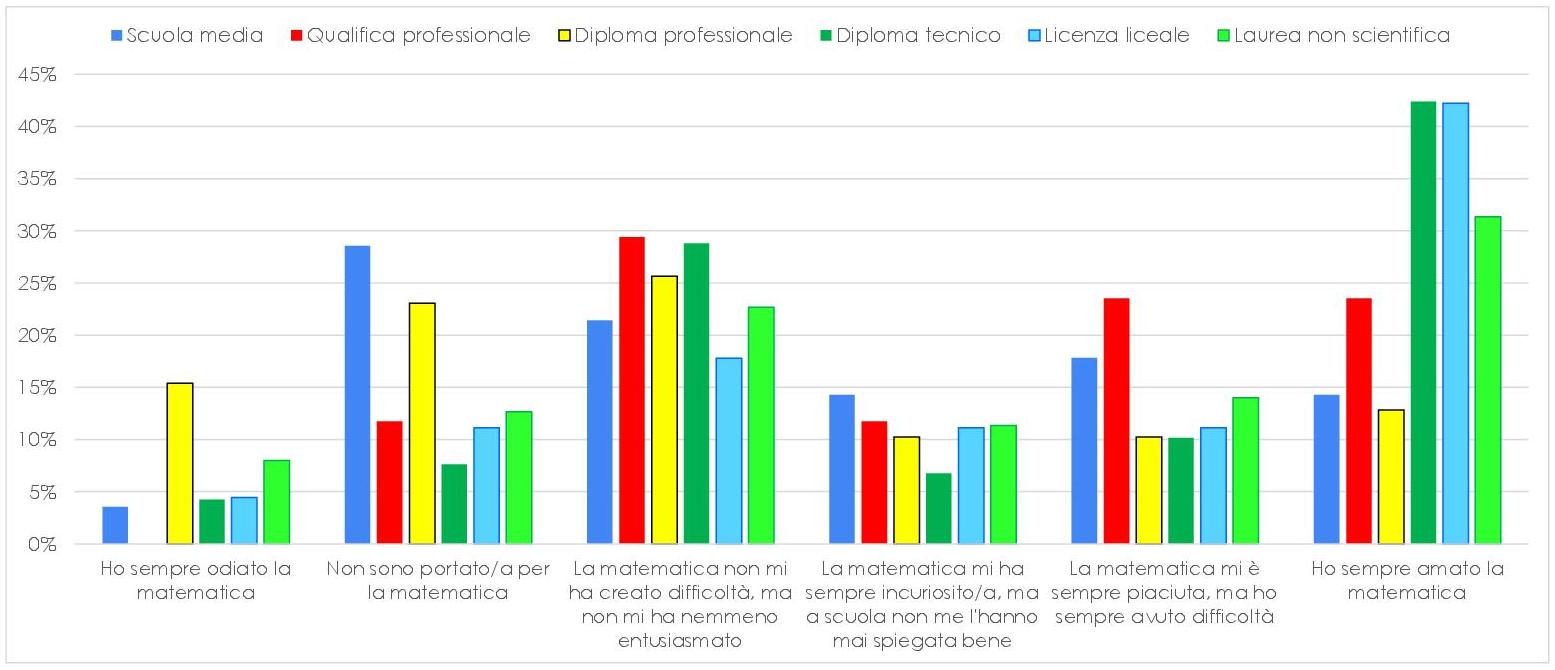
Nella stesura del questionario, abbiamo ritenuto importante indagare anche il rapporto dei partecipanti con la matematica e, suddividendo le loro risposte in base al grado di istruzione, abbiamo potuto trarre alcune conclusioni che, per quanto limitate al campione esaminato, sono interessanti e permettono alcune riflessioni di più ampio respiro.
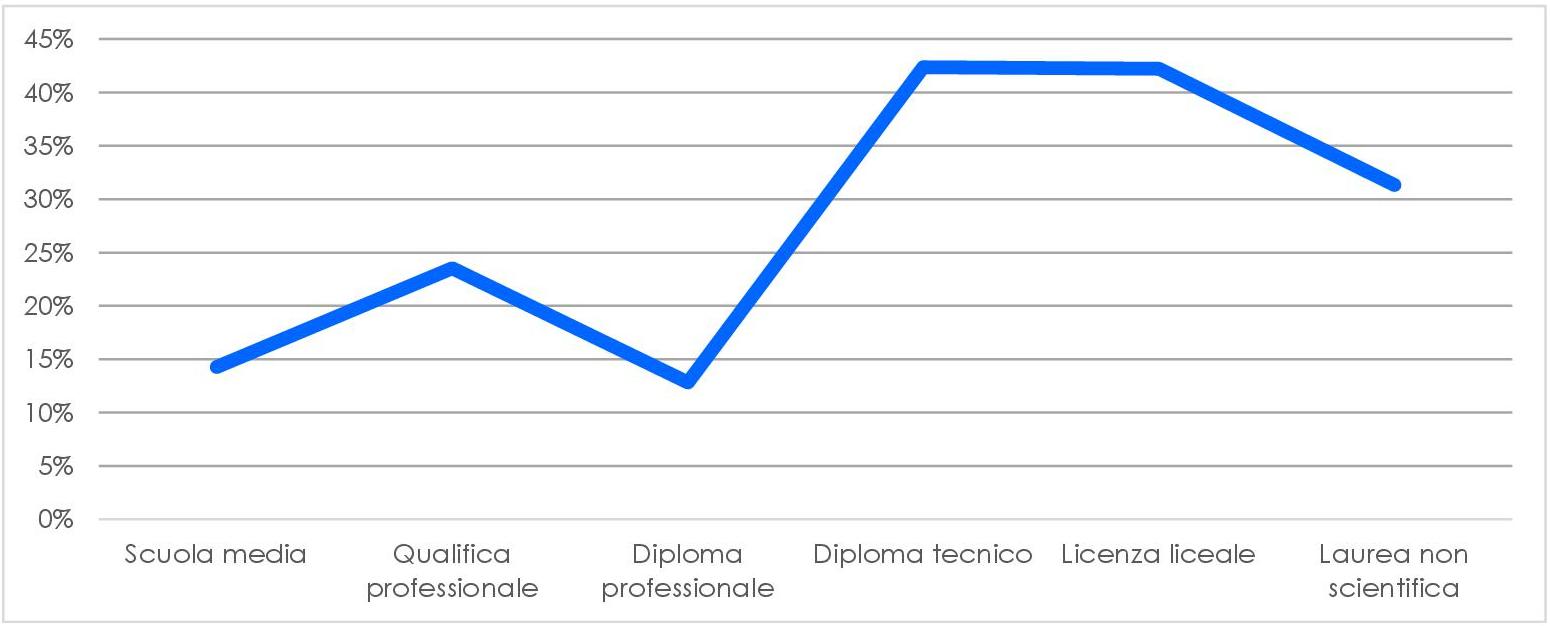
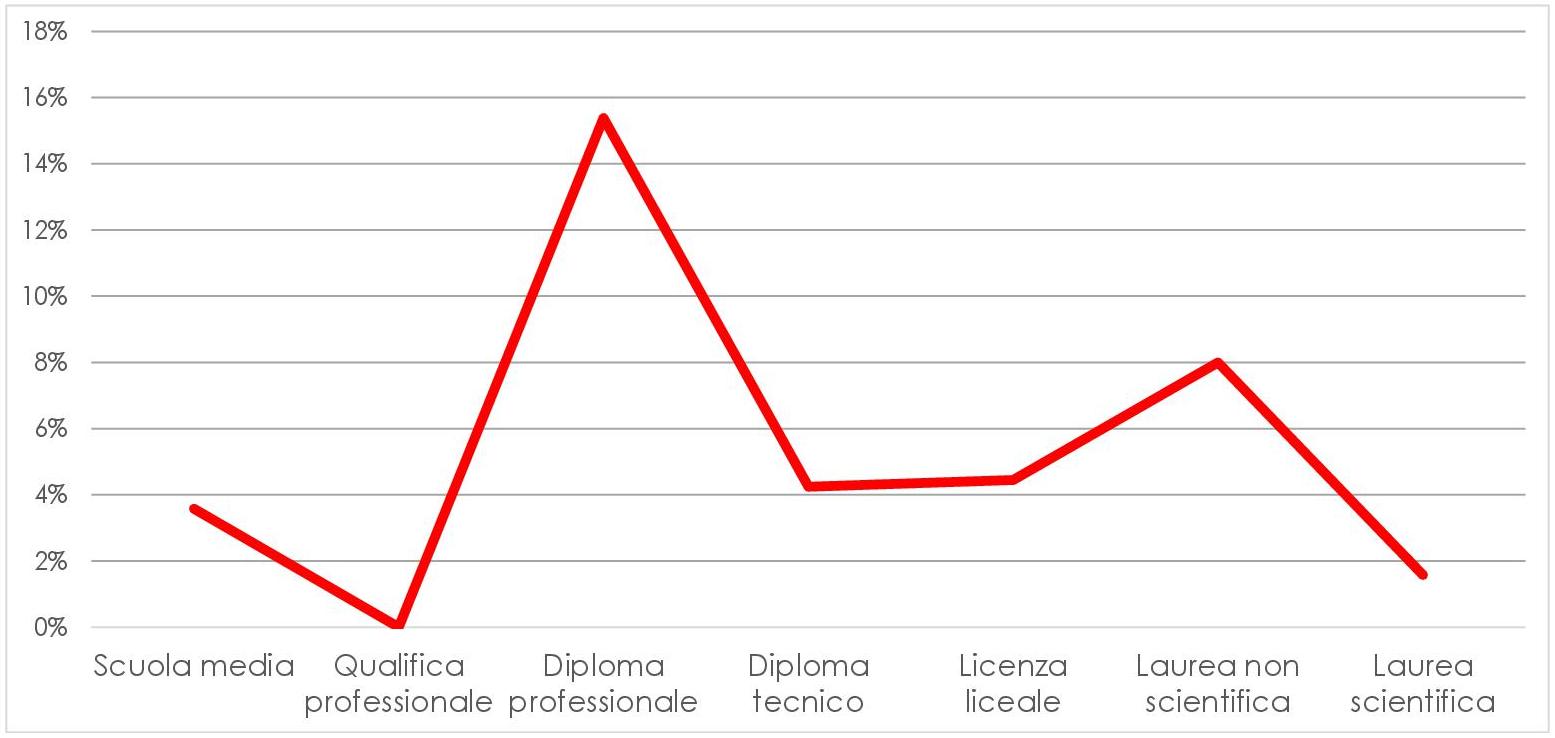
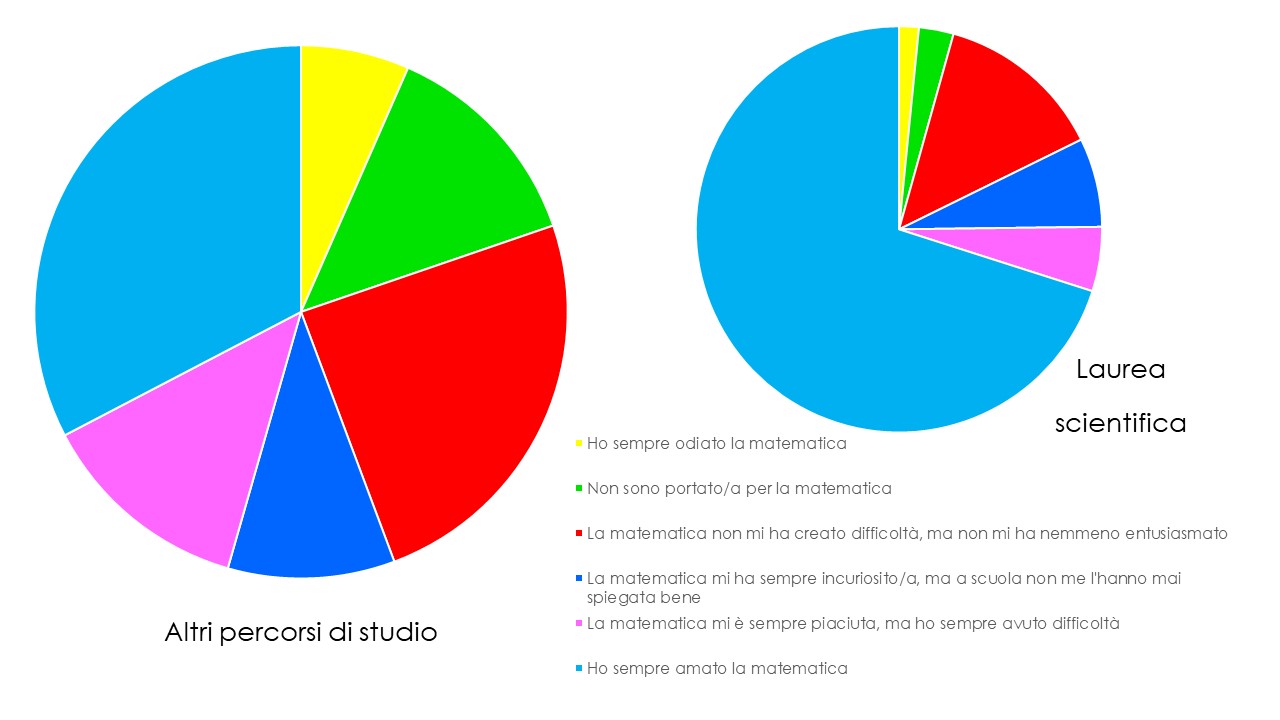
I due grafici precedenti si riferiscono all’amore (in blu) e all’odio per la matematica: tra i nostri intervistati, chi ha scelto di non proseguire gli studi dopo la scuola secondaria di primo grado ha avuto maggiori difficoltà in matematica e, in alcuni casi, ha sviluppato un sentimento negativo per la disciplina. Sorprendentemente, sulla totalità del campione solo il 5% ha dichiarato di odiare la matematica, mentre quasi la metà ha ammesso di averla sempre amata e molti hanno affermato di esserne stati affascinati o incuriositi. Questo ci ha portato a interrogarci sulle risposte raccolte e abbiamo dedotto che le risposte sono arrivate, di preferenza, da chi già aveva un sentimento positivo per la matematica: a parte i nostri contatti diretti, scelti tra i nostri genitori e gli amici dei nostri genitori, che hanno scelto di rispondere perché gliel’abbiamo chiesto noi, gli altri intervistati non sono stati scelti tra gli utenti dei social in generale, ma tra quelli che hanno già un rapporto positivo con la materia. Infatti, il questionario è stato condiviso dagli appassionati di matematica sui gruppi a tema matematico. Per questo motivo, per quanto il risultato possa essere più variegato quando si considerano altri percorsi di studio, rispetto alla laurea scientifica, anche in questo caso il nostro risultato non è attendibile: presenta una visione forse troppo rosea della realtà!
Non sorprende che chi ha conseguito una laurea scientifica abbia avuto un rapporto positivo con la matematica lungo il percorso, visto che il 60% degli intervistati ha dichiarato di essere stato influenzato nelle proprie scelte (scolastiche e lavorative) dal rapporto che ha avuto con la matematica. È per questo motivo che dal grafico che segue abbiamo dovuto escludere i laureati in materie scientifiche: l’elevata percentuale di amore per la matematica (70%) falsava la scala del grafico, appiattendolo, e rendendo, quindi, più difficile vedere le differenze tra le risposte dei singoli gruppi.
I SENTIMENTI DEI DOCENTI
Visto che tra i partecipanti all’indagine c’è un numero importante di insegnanti con laurea scientifica (86 questionari, corrispondenti al 13% degli intervistati), abbiamo deciso di analizzare in particolare il rapporto che essi hanno dichiarato di avere con la matematica e oltre ad aver raccolto 63 dichiarazioni di amore incondizionato per la materia, «Ho sempre amato la matematica», le risposte sono state un po’ più articolate, come se le possibilità concesse dal questionario non fossero adeguate ad esprimere la complessità del sentimento generato dalla matematica.
Oltre a quelli che hanno scelto più opzioni tra quelle proposte, qualcuno ha aggiunto particolari personali, a dimostrazione del fatto che la matematica genera sentimenti che coinvolgono il vissuto e che riconoscono addirittura una data all’inizio di questo amore: «Ho iniziato ad amare la matematica alle superiori grazie alla mia insegnante che ho avuto per tutti i cinque anni», «Ho iniziato ad amare la matematica dopo un'illuminazione ricevuta in seconda Liceo Scientifico», «Quando andavo a scuola non la amavo seppur non abbia mai avuto difficoltà. Poi qualcosa è cambiato!». Un altro commento rimanda a un rapporto con la matematica che non può che essere la traduzione di un rapporto con le persone, soprattutto alla primaria: «Ho sempre amato la matematica, ma me l'ha insegnata veramente bene solo la maestra; poi, un pochino, la professoressa delle medie; poi il nulla...», o come dichiarato da persone con altro titolo di studio: «La matematica mi piaceva, ma la professoressa era odiosa e quindi pure la matematica!». Per qualcuno questo amore ha rischiato di finire con l’esperienza universitaria: «Non mi ha entusiasmato lo studio universitario, tranne qualche esame, perché troppo teorico e nozionistico. Preferivo l'approccio più problematico, ragionato e applicativo del liceo scientifico», anche se abbiamo trovato un ingegnere che ha riportato un’esperienza opposta: «Ho scoperto la bellezza della matematica all’università. Fino alle superiori non mi è mai stata spiegata con passione da professori il cui unico obbiettivo era completare superficialmente il programma scolastico senza alcun amore per la professione dell’insegnante». Qualcuno, infine, dichiara un amore tardivo: «La matematica mi ha sempre affascinato e mi è sempre risultata piuttosto facile a scuola, però l’ho sempre studiata più per dovere che per passione finché ero studente».
Analizzando le risposte al nostro questionario, non è stato possibile individuare una professione con un vero odio per la matematica: in 34 questionari abbiamo registrato la risposta «Ho sempre odiato la matematica» e in 58 «Non sono portato/a per la matematica», ma non c’è una professione più presente di altre. Due sole sono le professioni che, in qualche modo, spiccano per una maggiore frequenza: quella degli impiegati (19 risposte in totale) e quella degli insegnanti (20 risposte). Questo non è sufficiente per dire che le due categorie sono "responsabili" di un sentimento particolarmente negativo per la disciplina, perché le due categorie spiccano anche nel sentimento opposto: semplicemente, siccome è elevato il numero di impiegati e di insegnanti intervistati, non possono che spiccare.
Tra le più belle risposte, non possiamo non segnalare quella di un’insegnante di religione di più di sessant’anni: «Subisco il fascino della matematica, riconosco che va avvicinata con creatività, penso che ci avvicini all'Infinito, ma so anche di non essere capace di inoltrarmi nella sua conoscenza». E questo solleva un importante tema, che ritorna più volte nelle risposte: non è l'odio il sentimento che ha raccolto il maggior numero di risposte, ma la sensazione di non essere portati per la matematica, il senso di inadeguatezza, o forse un facile alibi.
I SENTIMENTI DIVISI PER CATEGORIE PROFESSIONALI
Utilizzando la divisione per categorie di lavoratori come nel precedente paragrafo, abbiamo suddiviso le risposte in merito ai sentimenti della matematica.
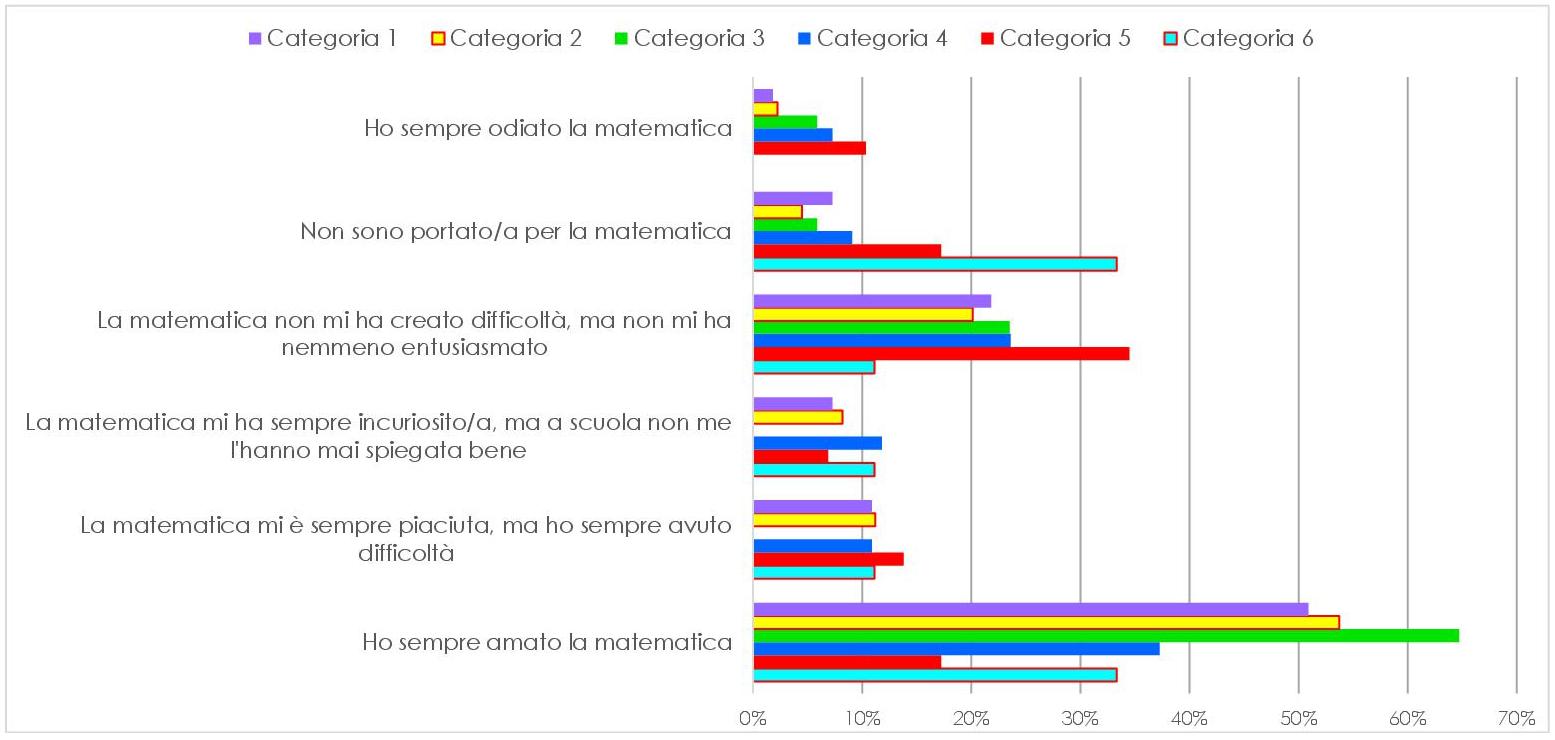
Quanto evidenziato dal grafico dà un’ulteriore conferma a quanto affermato precedentemente e, al tempo stesso, mostra come il riconoscimento dell’applicazione della matematica nelle proprie mansioni vada di pari passo con i sentimenti positivi che si possono nutrire per la disciplina. In alcune professioni, si sono rilevati risultati contraddittori in merito all’utilizzo della matematica, perché pur facendo lo stesso lavoro qualcuno ne ha riconosciuto la presenza e l’utilità, a fronte di altri che hanno dichiarato, quasi con spavalderia, di poterne fare a meno.
Prosegui con Conoscenze adeguate?
Matematica e mondo del lavoro
Per capire quanto la matematica sia presente nel mondo del lavoro, è stato necessario procedere con un raggruppamento delle professioni in alcune categorie, secondo la Nomenclatura e classificazione delle Unità Professionali dell’ISTAT, escludendo quelle risposte che non ci hanno fornito una risposta precisa o utile ai fini del sondaggio in questione come:
- pensionati, disoccupati e studenti: non è stato possibile associare loro una professione;
- liberi professionisti: si inseriscono in un ambito lavorativo molto vario e generico, difficile da classificare;
- insegnanti: l’insegnamento abbraccia molteplici e diverse discipline e spesso non è specificato il grado di scuola. Inoltre, l'elevato numero di questionari avrebbe falsato l'esito dell'indagine.
Le categorie risultanti sono sei:
- Categoria 1: legislatori, imprenditori e alta dirigenza (avvocati, direttori, dirigenti, manager, imprenditori, responsabili) Il primo grande gruppo, secondo l’ISTAT, «comprende le professioni che richiedono un livello di conoscenza necessario a definire e implementare strategie di indirizzo e regolazione in ambito politico, istituzionale ed economico, anche avvalendosi di contributi specialistici».
In questa categoria, abbiamo raccolto 55 questionari e tra di essi solo 9 dichiarano di poter svolgere il proprio lavoro senza la matematica. La maggior parte di chi ha risposto ritiene che la matematica faciliti il proprio lavoro, soprattutto gli imprenditori (74%), che sono gli unici a non aver risposto di poter fare a meno della matematica.
- Categoria 2: professioni intellettuali, scientifiche e di elevata specializzazione (data scientist, ingegneri, consulenti, architetti, psicologi, bibliotecari, ricercatori, informatici, infermieri, farmacisti, commerciali, commercialisti, medici e fiscalisti). «Il secondo grande gruppo comprende le professioni che richiedono un elevato livello di conoscenza teorica per analizzare e rappresentare, in ambiti disciplinari specifici, situazioni e problemi complessi, definire le possibili soluzioni e assumere le relative decisioni. I loro compiti consistono nell’arricchire le conoscenze esistenti.»
In questa categoria, abbiamo raccolto 134 questionari e tra di essi abbiamo la maggioranza assoluta della risposta «il mio lavoro non esisterebbe senza matematica». Anche osservando il grafico più dettagliato, possiamo concludere che tutte le professioni necessitano della matematica.
- Categoria 3: professioni tecniche (geometri, educatrici, agenti commerciali e un pilota di linea). «Il terzo grande gruppo comprende le professioni che richiedono conoscenze tecnico-disciplinari per selezionare e applicare operativamente protocolli e procedure definiti e predeterminati in attività di produzione o servizio. I loro compiti consistono nel coadiuvare gli specialisti in ambito scientifico, sanitario, umanistico, economico», sociale e produttivo.
In questa categoria, abbiamo raccolto 17 questionari, ma la maggior parte (11) è stata compilata da educatori, falsando quindi il risultato. Geometri, agenti di commercio e piloti non avrebbero un lavoro senza la matematica. Se analizziamo anche gli argomenti in gioco, scopriamo che gli educatori usano solo nozioni di calcolo aritmetico, mentre gli altri professionisti – i geometri in particolare – fanno uso non solo di grafici, ma anche di teoremi di geometria.
- Categoria 4: professioni esecutive nel lavoro d’ufficio (impiegati). La quarta categoria «comprende le professioni che svolgono il lavoro d’ufficio con funzioni non direttive. I loro compiti consistono nell’acquisire, trattare, archiviare e trasmettere informazioni […] e nella verifica e corretta applicazione di procedure».
In questa categoria, abbiamo raccolto 110 questionari e a parte 8 risposte, tutte le altre riconoscono la matematica come fondamentale nel proprio lavoro. Come indicato dall’ISTAT, le attività svolte consistono nell’amministrazione del personale, nel gestire la circolazione del denaro, nell’effettuare calcoli e rendicontazioni statistiche, e, per questo motivo, la maggior parte degli impiegati non può che riconoscere che senza matematica non avrebbe un lavoro.
Questa categoria, per la quale abbiamo realizzato un unico grafico visto che comprende un’unica figura professionale anche se dalle attività diversificate, rappresenta circa un sesto dei questionari analizzati: non è un caso, visto che le figure indagate lavorano nel settore terziario, che è uno dei settori più sviluppati in Italia.
- Categoria 5: professioni qualificate nelle attività commerciali e nei servizi (hair-stylist, pasticceri, commesse e commercianti). «Il quinto grande gruppo classifica le professioni che assistono i clienti negli esercizi commerciali, forniscono servizi di ricezione e di ristorazione, servizi ricreativi e di supporto alle famiglie, di cura della persona, di mantenimento dell’ordine pubblico, di protezione delle persone e della proprietà».
In questa categoria, abbiamo raccolto 29 questionari, dei quali 10 tra le casalinghe, che dichiarano, in buona parte, di poter fare a meno della matematica, o di poterlo fare con un po’ di fatica. Per i commercianti, le commesse, e l’unico pasticcere intervistato, la matematica è presente e davvero importante per il lavoro.
- Categoria 6: artigiani, operai specializzati e agricoltori (falegnami e operai). «Il sesto grande gruppo comprende le professioni che utilizzano l’esperienza e applicano la conoscenza tecnico-pratica dei materiali».
Tra i 9 questionari raccolti ci sono 8 operai e un falegname: per gli operai metalmeccanici la matematica è importante, come pure per il falegname, mentre tra gli altri operai due affermano di poter fare a meno della matematica.
Tra le risposte che ci sono pervenute, c’erano anche tre poliziotti, che abbiamo inserito nella categoria 5, perché sarebbe stato poco significativo considerarli nella loro categoria di appartenenza (la 9); non abbiamo trovato nessuno né per la categoria 7 né per la 8, anche se alcuni elementi – pochi – avrebbero potuto essere inseriti in queste. Abbiamo preferito ridurre tutto a sei categorie per rendere più facile lo studio.
Osservando i dati raccolti, ci rendiamo conto ora che la nostra indagine avrebbe dovuto cominciare dalla scelta degli intervistati: avremmo dovuto puntare ad avere lo stesso numero di elementi in tutte le categorie, ma la verità è che tutto è cominciato come una piccola indagine tra i nostri conoscenti e mai avremmo pensato di dover analizzare tanti questionari. Fin dall'inizio abbiamo riconosciuto che il nostro campione non è statisticamente rappresentativo, ma a noi è bastato per gettare uno sguardo sul mondo del lavoro e sul ruolo della matematica al suo interno.
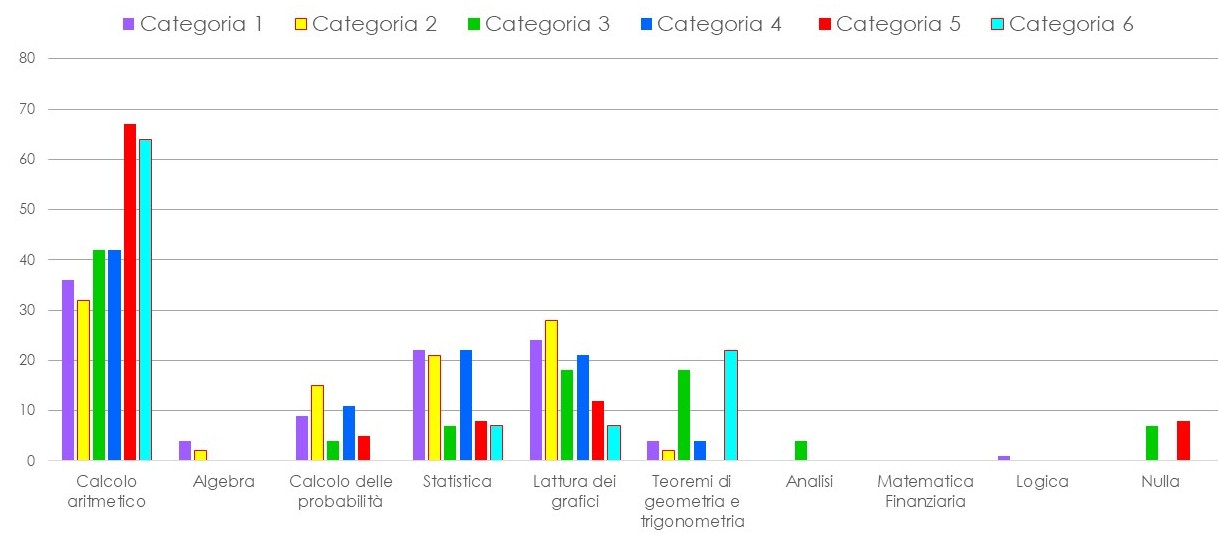
QUALE MATEMATICA?
Calcolo aritmetico, algebra, calcolo delle probabilità e statistica, lettura dei grafici, teoremi di geometria e trigonometria, analisi e logica sono le parti della matematica più usate nelle varie professioni e, come è evidente dal grafico, ogni professionista necessita di matematica, per poter svolgere al meglio la propria mansione.
Come era prevedibile, il calcolo aritmetico è quello più usato da tutte le categorie: è indispensabile, non solo in termini di addizioni e sottrazioni. Tendiamo a classificare come “banale” calcolo aritmetico tutta quella matematica che ci pare semplice, ma sappiamo che anche il calcolo di una percentuale, per quanto comporti la soluzione di una semplice proporzione, non è così scontato. La lettura di grafici diventa determinante nell’ambito decisionale, come dimostrato dalle risposte delle categorie dirigenziali, mentre l’uso dei teoremi di geometria non è limitato alla categoria degli ingegneri e dei geometri, perché anche il falegname può averne bisogno.
Tra le risposte, ci ha colpito molto quella di una data scientist: "calcolo aritmetico, statistica, lettura di grafici, trigonometria (una sola volta, ma fu determinante)". Questa risposta ci ha fatto riflettere: nessuno di noi può sapere cosa sarà utile, di ciò che studiamo oggi, nel mondo del lavoro, ma tutto potrebbe essere utile, o addirittura necessario, "determinante". Non abbiamo ancora le idee chiare sulle nostre scelte lavorative, ma in ogni caso, nemmeno questa data scientist avrebbe potuto immaginare che avrebbe avuto bisogno della trigonometria!
In conclusione, possiamo affermare che nonostante l’utilizzo delle diverse parti della matematica fatto dalle diverse professioni sia abbastanza diversificato e sia specifico, a volte, per alcune mansioni, tutte le professioni fanno uso di matematica.
QUANTO È IMPORTANTE LA MATEMATICA NEL MONDO DEL LAVORO?
Per analizzare l’importanza della matematica nel mondo del lavoro, facciamo riferimento alla domanda 8 e facciamo una media dei valori assegnati da ogni intervistato. Riportati i risultati in un grafico, possiamo notare come la categoria 5, formata da 29 persone che compiono lavori pratici, sia quella che dà meno importanza alla matematica, facendone un utilizzo, per certi aspetti, più limitato. Per quanto riguarda la categoria 3, secondo risultato partendo dal basso, abbiamo già riconosciuto che la mescolanza delle professioni tecniche ha generato dei risultati un po’ bizzarri.
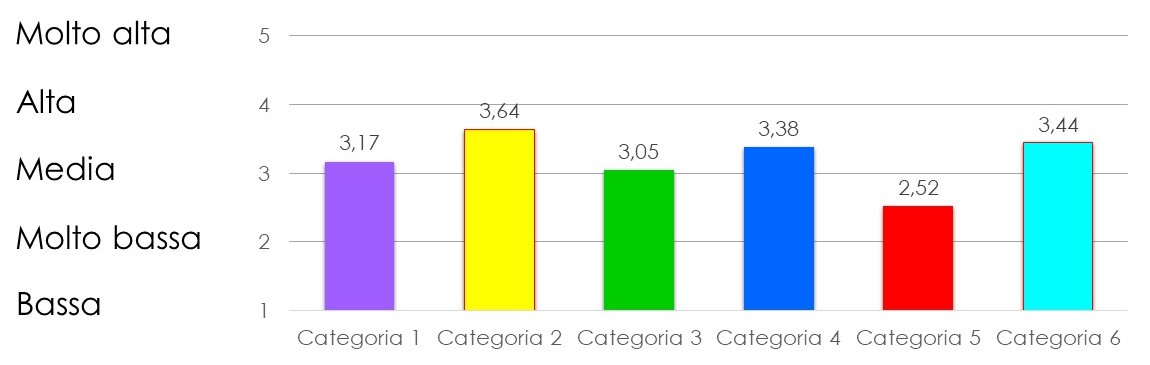
Rispetto alle domande analizzate in precedenza, possiamo rilevare una certa coerenza, tranne che per le categorie con il più basso numero di questionari: in questo caso, anche una singola risposta può incidere significativamente sui risultati medi.
Dall’analisi dei dati, possiamo dedurre che:
- La matematica è presente in tutti gli ambiti lavorativi;
- Gli strumenti matematici utilizzati sono condivisi da tutte le categorie, visto che solo alcuni settori particolari usufruiscono di metodologie logico-matematiche più settoriali;
- Chi potrebbe fare a meno della matematica si ritroverebbe con un lavoro più pesante e faticoso
- Abbiamo anche notato alcune incongruenze: in alcuni casi, pur svolgendo la stessa identica professione, è stato segnalato un uso diverso della matematica: a seconda della formazione della persona in questione (ad esempio: al livello dirigenziale si può accedere sia con una laurea scientifica che con una laurea non scientifica) è stata riconosciuta una presenza o un'assenza di matematica. In altre parole, parafrasando una celebre citazione: la matematica è negli occhi di chi guarda.
Prosegui con Il rapporto con la matematica
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy
