Tutto è cominciato un giorno d’estate, quando, sfogliando la rivista Sapere (della casa editrice Dedalo), mi sono imbattuta nella rubrica “Homo Mathematicus” tenuta da Roberto Natalini, coordinatore del sito MaddMaths!, matematico applicato, dirigente dell’Istituto per le Applicazioni del Calcolo del CNR e divulgatore con MaddMaths!, Archimede e Comics&Science. La rubrica, nel numero 3/2025, si intitolava: Il segreto dei matematici. 

Invitato al compleanno della piccola Renata, Roberto Natalini, da matematico, osserva, analizza, riflette. Tutto comincia con il gioco che ha scelto di regalare alla piccola duenne, che si mescola, nella sua testa, con il libro scritto dal matematico francese David Bessis. Roberto riflette sul fatto che non siamo nati sapendo già fare le cose, perciò siamo “costretti” a imparare ciò che ci serve, una cosa alla volta. La stessa cosa avviene con la matematica, che pare un lento aprirsi al nuovo: «Avete capito il trucco, una nuova idea, quella di “forma” che si è creata nella vostra mente.» Anche Odifreddi nel libro Perché studiare matematica (non) è impossibile parla di crescita: «La capacità matematica, che richiede il ragionamento logico-deduttivo, ovvero la capacità di partire da delle ipotesi per trarre delle conclusioni, si sviluppa per ultima. […] Quindi è chiaro che spesso risulti difficile, se non impossibile, capire alcune cose, alcuni passaggi o ragionamenti.»

Questa crescita non può avvenire senza cambiare punto di vista, perché il cambio di prospettiva aiuta a vedere le cose in modo più completo, più vero, anche se è difficile individuare la verità. Roberto Natalini scrive: «Un’intuizione che viene da un cambiamento di punto di vista e che solo dopo, con pazienza, riuscirete a spiegare agli altri, a trovarne la regola, a formalizzare.»

Nell'articolo, Roberto Natalini propone quello che, come matematico, considera il segreto dei matematici e io, che la matematica la insegno ma non la pratico, provo a proporre la mia idea di segreto.

Il segreto del matematico potrebbero essere le definizioni? 
Odifreddi scrive: «Anzitutto si parla di cose che vengono premesse agli inizi. Le definizioni sono il punto di partenza.» Penso a una delle definizioni più difficili della matematica, quella di limite, e realizzo che, per quanto difficile, nessuna definizione matematica potrà eguagliare le definizioni giuridiche, come quella di genocidio, ad esempio. Inserita nella Convenzione per la prevenzione e la repressione del delitto di genocidio, un trattato approvato dall’Assemblea generale dell’ONU nel 1948, la definizione di genocidio è riconosciuta a livello internazionale. Eppure non è così facile stabilire se un certo fenomeno rientri nella definizione oppure no.

Forse il segreto del matematico risiede nei postulati? 
Sempre Odifreddi scrive: «La matematica non è la ricerca di una verità assoluta. Perché in matematica tutto è relativo rispetto ai punti di partenza che vengono scelti, ovvero i postulati.» Un postulato in particolare, il quinto postulato degli Elementi, non riconosciuto come ovvio, viene messo alla prova con una dimostrazione per assurdo, che porterà alle Geometrie non euclidee, ottime per descrivere il mondo attorno a noi.

Il segreto del matematico sono le dimostrazioni? 
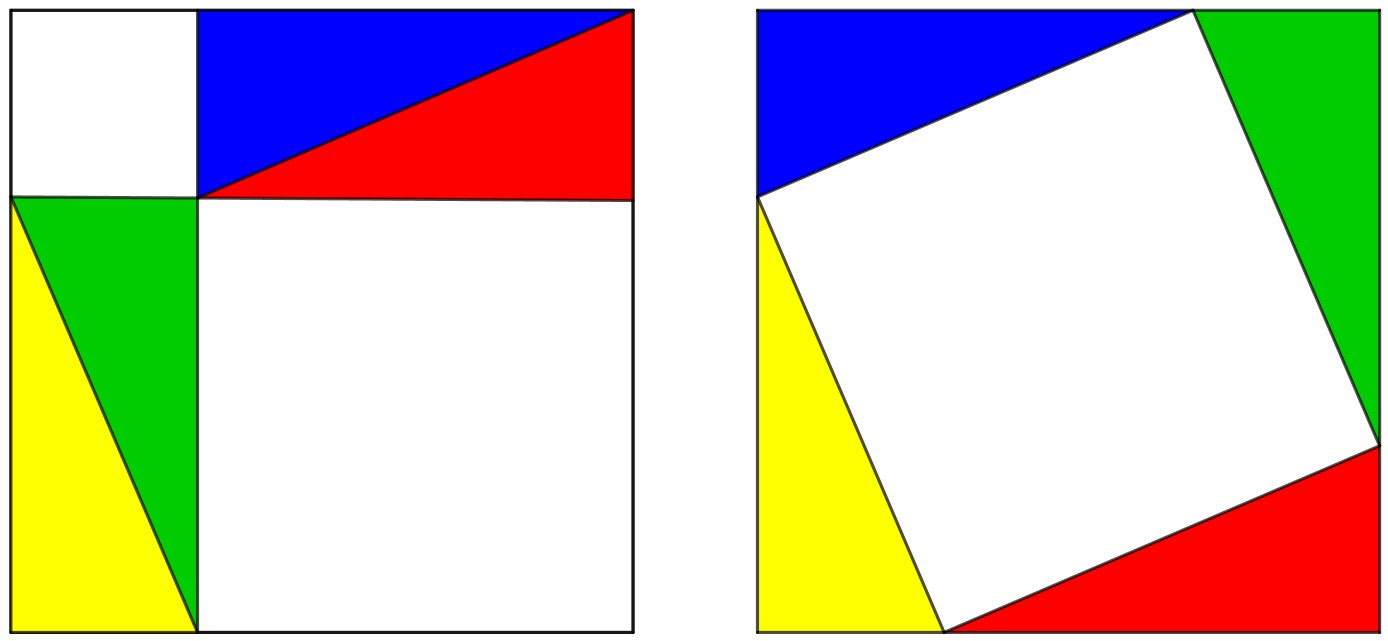
Odifreddi ci spiega che «Per la matematica, a una stessa cosa ci si può arrivare in modi diversi.» A tal proposito, la dimostrazione del teorema di Pitagora è un ottimo esempio, visto che ci sono centinaia di dimostrazioni diverse, compresa una di Leonardo da Vinci e del presidente statunitense Garfield. Potremmo illuderci che, qualunque sarà la domanda, ci sarà sempre un matematico che potrà trovare la risposta, che potrà stabilire se quanto richiesto sia vero o falso. In altre parole, una congettura potrà essere dimostrata, e quindi diventare un teorema, o se ne troverà un controesempio, che ne sancirà la falsità.

Ma le cose non stanno proprio così: forse sarebbe preferibile scegliere, come segreto del matematico, l’incompletezza. 
Nel 1930 Gödel enunciò il suo primo teorema di incompletezza durante una tavola rotonda a margine della Seconda Conferenza sull’epistemologia delle scienze esatte di Königsberg. «Ci saranno sempre domande cui non c’è risposta», dichiara, in altre parole ci sono enunciati non dimostrabili. «È la fine», commenta von Neumann, che si trova tra il pubblico insieme a Russell. «So che è difficile per i profani comprendere… ma per molti eccellenti studiosi il Teorema di Incompletezza significava la fine di un sogno!», come succede ad Hilbert, ad esempio.

A questo punto del percorso, forse, può sorgere una ulteriore domanda: ma il segreto del matematico è la razionalità, come pensano tutti, o la follia? Nel libro Logicomix il legame tra la logica e la follia viene esplorato in ogni direzione. Mi limito a citare le vicende di Cantor o di Gödel: il primo soffrì di attacchi di depressione, che arrivarono a compromettere le sue abilità di matematico e lo portarono a morire in un ospedale psichiatrico, mentre per il secondo la morte è legata a un disturbo ossessivo-compulsivo degenerato in delirio paranoico, e una grave forma di anoressia.

Mentre la mente comincia a vacillare, ecco un nuovo segreto: possono essere un segreto dei matematici i paradossi? 
Bastano poche parole per confondere le acque: pensiamo al paradosso di Eubulide, “Miei cari cittadini… io sto mentendo!” «Se lui sta mentendo, allora sta dicendo la verità! E se sta dicendo la verità… allora sta mentendo!» E il paradosso di Russell? «Immaginate una città in cui vige una legge molto ferrea che impone a tutti gli adulti maschi di radersi quotidianamente. Ma non li obbliga a radersi da soli e quelli che non lo fanno da soli devono andare dal barbiere. Infatti, la legge dice: “Coloro che non si radono da soli verranno rasati dal barbiere”. […] Chi rade il barbiere? Ovviamente non può farlo lui, perché…»

Parlando di matematica non si può non lasciarsi sopraffare dal fascino dell’infinito. Che sia questo il segreto?
In realtà, anche in questo caso si finisce con l’imbattersi in un paradosso, quello dell’albergo infinito di Hilbert. Basta solo che gli ospiti accettino di cambiare stanza e si trova un posto per tutti, che arrivi una sola persona in più, che ne arrivi un pullman infinito o che arrivino infiniti pullman infiniti… Nell’albergo di Hilbert nessuno si ritrova a dormire sul pavimento!

Insomma, a me comincia a girare la testa: abbiamo esplorato la strada delle definizioni, quella dei postulati, con quella delle dimostrazioni siamo approdati all’incompletezza e da lì il passo verso la follia, o la razionalità, è stato breve, e ci ha mostrato i paradossi, mentre ci mancava l’aria di fronte all’infinito. Potremmo continuare ancora a lungo, pensando al simbolismo, alla disciplina necessaria per studiarla, potremmo pensare a quel rigore che tanto spaventa gli alunni, ma ciò con cui si scontrano realmente è quello che viene messo in evidenza anche da Odifreddi: «In matematica non si bara. Non si può barare perché si viene scoperti subito. [...] Se la risposta è quella, è quella. Se la risposta è sbagliata, è sbagliata. E questo può dare fastidio perché richiede disciplina.»

Comincia a girarmi la testa e realizzo che, per quanto i matematici riescano a vedere la matematica ovunque, non significa che abbiano degli occhiali speciali, o che riescano ad evitare gli errori. Ogni risposta che ho tentato di dare è, a suo modo, un pezzo della verità. Alla fine, prima di dare la mia risposta, cerco quella dei miei studenti di quinta liceo scientifico, perché, in realtà, questo lungo percorso non è stato altro che la prima lezione di matematica dell'anno!

Dedizione, passione, impegno, determinazione e perseveranza la fanno da padrone, il riferimento alla “pazzia fantasiosa” e al fatto che si tratti di “guardare e ragionare sul mondo con occhi di follia” mostrano che le vicende di Cantor e di Gödel che ho raccontato hanno colpito nel segno, mentre qualcuno ipotizza che per il matematico sia importante collegare la logica al tempo. Dopo i modelli, la curiosità, l’astrazione e il riposo (anche l’immagine di un Edison addormentato* mentre è a un picnic con il presidente degli Stati Uniti Warren Harding, che ho presentato come invito ad essere capaci di staccare, ha lasciato il segno) qualcuno si avvicina alla mia idea di segreto, scrivendo “tentativi continui” e “non mollare davanti alle difficoltà”.

Per me, il segreto del matematico è quello di sentirsi sfidato dalla difficoltà: il matematico non si tira indietro di fronte alla difficoltà, ma si comporta come Jannik Sinner, che di fronte alla sconfitta agli US Open dice di aver trovato una nuova strada. Da questo punto di vista, la sconfitta non è un fallimento ma un’opportunità per riuscire a fare meglio. E se Sinner pare fuori luogo in un contesto matematico, lasciamo la parola a Einstein: «La creatività nasce dall’angoscia come il giorno nasce dalla notte oscura. È nella crisi che sorge l’inventiva, le scoperte e le grandi strategie. Chi supera la crisi supera se stesso senza essere superato.»

* citazione dal libro di Mario Calabresi Il tempo del bosco